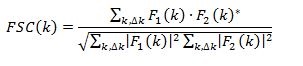“图像处理(图像处理、波形处理)”的版本间的差异
(→18-1. Fourier transform) |
(→27. Fourier Shell Correlation, FSC) |
||
| (未显示同一用户的6个中间版本) | |||
| 第90行: | 第90行: | ||
Young fringe</pre> | Young fringe</pre> | ||
===18-3.inverse Fourier transform=== | ===18-3.inverse Fourier transform=== | ||
| − | Fourier transform is a method that transforms a function of certain variables into the function of the variables conjugate to the certain variables. On the other hand, "inverse Fourier transform" is a method that transforms the Fourier-transformed function into | + | Fourier transform is a method that transforms a function of certain variables into the function of the variables conjugate to the certain variables. On the other hand, "inverse Fourier transform" is a method that transforms the Fourier-transformed function into a function of the original variable. For example, when a crystal potential as a function of position is Fourier-transformed, crystal structure factors are obtained as a function of wavenumber. Next, when the crystal structure factors are inverse-Fourier-transformed, the crystal potential as the function of position is obtained. In TEM imaging, Fourier transform and inverse Fourier transform of the specimen are automatically executed, so that the diffraction pattern and structure image are obtained at the back focal plane and the image plane, respectively. |
<pre>Related term | <pre>Related term | ||
Fourier transform</pre> | Fourier transform</pre> | ||
| + | |||
==19. Fourier mask== | ==19. Fourier mask== | ||
The "Fourier mask" is a mask inserted on the diffraction plane to remove the noise of a lattice image or a structure image, allowing only diffraction spots to pass and background noise between the diffraction spots to be cut. | The "Fourier mask" is a mask inserted on the diffraction plane to remove the noise of a lattice image or a structure image, allowing only diffraction spots to pass and background noise between the diffraction spots to be cut. | ||
| 第124行: | 第125行: | ||
<pre>Related term | <pre>Related term | ||
curve fitting, Gaussian function, Lorentzian function</pre> | curve fitting, Gaussian function, Lorentzian function</pre> | ||
| + | ==27. Fourier Shell Correlation, FSC== | ||
| + | Fourier Shell Correlation (FSC) is a measure of reliability of the three-dimensional (3D) structures of biological macromolecules obtained by “single particle analysis”. FSC is expressed as a function of spatial frequency by the following equation (normalized cross correlation). | ||
| + | |||
| + | [[文件:Fourier-shell-correlation 01.jpg]] | ||
| + | |||
| + | Here, F1(k) and F2(k)are 3D Fourier transforms of the two structures reconstructed from arbitrary two independent sets of TEM images obtained. F2(k)* is a complex conjugate of F2(k), and Σk,ΔkF(k) means summing up F(k) over a small range Δk around k. | ||
| + | FSC (k) takes a value between +1 and –1 for every spatial frequency k. The value of FSC (k) close to +1 means that the two reconstructed structures agree well, indicating a high degree of reliability of the obtained structure. If FSC does not decrease monotonically with spatial frequency k at high frequencies, the reliability of the FSC function is considered to be low. | ||
| + | The following example shows the FSC and spatial resolution for mouse apoferritin. | ||
| + | First, a data set of TEM images acquired for single particle analysis is randomly divided into two groups, and two independent 3D structures are obtained by image-processing analysis for each group. FSC is calculated using the two obtained 3D structures. | ||
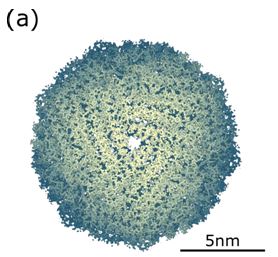
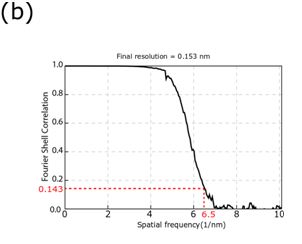
| + | Fig. 1(a) shows a 3D density map of apoferritin reconstructed from 120,295 particles extracted from 840 cryo-TEM images. Fig. 1(b) is the FSC calculated for this 3D density map. The values of FSC at low frequencies are close to +1 and damped with increasing frequency monotonically towards 0. This behavior confirms high reliability of the FSC function. | ||
| + | In single particle analysis, it is common to define the spatial resolution of the obtained structure to be the reciprocal of the spatial frequency at which FSC = 0.143. (The value “0.143” is a value adopted based on statistical discussion about the correlation of random noise and on referring the resolution defined for X-ray crystallography.) The resolution for apoferritin was determined to be 0.153 nm from a spatial frequency of 6.5 nm-1 at which FSC takes a value of 0.143. | ||
| + | (Proofread by Specially Appointed Professor Keichi Namba, Osaka University) | ||
| + | [[文件:Fourier-shell-correlation 02.JPG]] [[文件:Fourier-shell-correlation 03.JPG]] | ||
| + | |||
| + | Fig1. 3D density map of mouse apoferritin obtained by single particle analysis and its FSC. (a) 3D density map. (b) An FSC function calculated from the two 3D density maps. The resolution was determined to be 0.153 nm from a spatial frequency of 6.5 nm-1 at which FSC = 0.143. | ||
2020年3月23日 (一) 07:31的最新版本
图像处理(图像处理、波形处理)
目录
- 1 1. fast Fourier transform
- 2 2. Gaussian function
- 3 3. gamma curve
- 4 4. inverse Fourier transform
- 5 5. calibration curve
- 6 6. least-squares method
- 7 7. Graphical User Interface (GUI)
- 8 8. auto-correlation function
- 9 9. cross-correlation function
- 10 10. first principle calculation
- 11 11. deconvolution
- 12 12. radial distribution function
- 13 13. noise filter
- 14 14. high-pass filter
- 15 15. curve fitting
- 16 16. Hough transform
- 17 17. Fourier synthesis
- 18 18. Fourier transform
- 19 19. Fourier mask
- 20 20. smoothing
- 21 21. maximum entropy method
- 22 22. Monte Carlo method
- 23 23. Radon transform
- 24 24. Richardson-Lucy method
- 25 25. low-pass filter
- 26 26. Lorentzian function
- 27 27. Fourier Shell Correlation, FSC
1. fast Fourier transform
A computing method to decrease the calculation time of a Fourier transform. Since "fast Fourier transform (FFT)" is executed using a computer, calculations are performed by a discrete finite sum, instead by an integration. It greatly decreases the computation time by dividing the calculation into certain sub-groups and by changing the order of the calculation. In a discrete Fourier transform with a period of N, the number of operation is normally proportional to N2 but it is decreased to N log N in FFT. This method is used for analysis of high-resolution images.
Related term Young fringe
2. Gaussian function
2-1. Gaussian function
"Gaussian function" is a function given by a exp { - (x - b)2 / c2}, where a, b and c are constants. It is used for pre-processing of the background in a spectrum and for fitting of the spectral intensity. Compared with the "Lorentzian function," the Gaussian function damps a little quickly in its tail. Real spectral shapes are better fitted with the Lorentzian function. However, the Gaussian function is conveniently used because it is manipulated mathematically easier than the Lorentzian function.
Related term curve fitting, Lorentzian function
2-2. mixed Gaussian/Lorentzian function
"Mixed Gaussian-Lorentzian function" is a function composed of a Gaussian and a Lorentzian function. It is used for pre-processing of the background in a spectrum and for fitting of the spectral intensity when the both functions are inappropriate to reproduce an experimental spectrum.
Related term curve fitting, Gaussian function, Lorentzian function
3. gamma curve
A "gamma curve" is an intensity compression curve for an observed intensity distribution to compress to a visual range when the intensity of a TEM image or a CBED pattern has a large dynamic range.
4. inverse Fourier transform
Fourier transform is a method that transforms a function of certain variables into the function of the variables conjugate to the certain variables. On the other hand, "inverse Fourier transform" is a method that transforms the Fourier-transformed function into the function of the original variable. For example, when a crystal potential as a function of position is Fourier-transformed, crystal structure factors are obtained as a function of wavenumber. Next, when the crystal structure factors are inverse-Fourier-transformed, the crystal potential as the function of position is obtained. In a TEM, Fourier transform and inverse Fourier transform of the specimen crystal are automatically executed, so that the diffraction pattern and structure image are obtained at the back focal plane and the image plane, respectively.
Related term Fourier transform
5. calibration curve
A "calibration curve" provides the responses of a physical property to a certain variable as a curve. For example, if a calibration curve between the concentration of an element and the intensity of the X-ray emission from the element is provided in advance, the quantitative measurement of the element in a substance can be carried out from a measured X-ray emission intensity.
6. least-squares method
"Least-squares method" is a method to determine unknown parameters so that the sum of squares of the residuals between the experimental and calculated values is minimized. It is used for crystal structure analysis and spectral curve fitting. When the sum of the squares of the residuals is minimized by a liner combination of unknown parameters (∑ai・xi + b), the method is called linear least-squares method. When a nonlinear function is used for fitting, it is called nonlinear least-squares method. Nonlinear least-squares method includes cases where fitting of unknown parameters is executed by numerical calculations without assuming a specific nonlinear function. For example, nonlinear least-squares fitting is effectively used to obtain structural parameters (atom positions, Debye-Waller factors) by minimizing the sum of the squares of the residuals between the experimental intensities of CBED patterns and the calculated intensities for crystal structure models. That is, the sum of the squares of the residuals for a set of certain structural parameters is obtained. Then, a set of structural parameters is generated so that the differential of the sum is negative with respect to each parameter. Then the sum of the squares of the residuals is calculated for the set of the generated parameters. Repeating the calculation procedure reaches the minimum sum of the squares of the residuals, determining the unknown parameters.
7. Graphical User Interface (GUI)
"GUI" is a user interface that provides intuitive operations using a computer graphics and a pointing device. Since GUI offers user-friendly operation and high visualization, it is widely used as a major interface for commercial OS. In the TEM, GUI is used to facilitate instrument operation and display of image-data. It is, however, noted that GUI is not always effective because different operations cannot be carried out simultaneously.
8. auto-correlation function
"Auto-correlation function" is a function to give information about the shape of the function such as sharpness, roundness, periodicity, etc. It is a function (or a pattern) that is acquired by integrating the product (overlap) of two same functions with respect to a variable which are shifted each other by a certain amount about the variable. That is, when we define the object function f, an integral variable of the function X and a relative shift of the function x, the auto-correlation function Rff can be written as the following equation: Rff=∫f(X)f*(X-x)dX. Note that * denotes complex conjugate. In the case of a microscope image etc., f is a real function and then f*(X-x)=f(X-x). If the value of Rff is large even for a large shift, the original function (or the original pattern) is delocalized in the X direction. Contrary, if the auto-correlation function decreases rapidly with increasing the relative shift, the original function (or the original pattern) is localized. If the function is peridic, Rff takes a large value at integral multiples of a certain x. Thus, the periodicity of the function is obtained. Therefore, the auto-correlation function enables us to obtain the knowledge about the shape of the function or the pattern with respect to the variable. For example, by calculating the auto-correlation function of a TEM image of a particle, the amount of deocus is estimated from a blur of the image and the amount of 2-fold astigmatism is obtained from an elongation of the image. For high-speed computer calculation of the auto-correlation function, FFT (fast Fourier transform) is used on the basis of the following theorem: Fourier transform of the product of certain functions is equivalent to the product of Fourier transforms of the respective functions. That is, the auto-correlation function is calculated by the inverse Fourier transform of the power of the Fourier transforms of the respective functions.
Related term cross-correlation function
9. cross-correlation function
"Cross-correlation function" is a function expressing to what extent arbitrary two functions are similar or to what extent the two functions are shifted. It is a function (or a pattern) that is acquired by integrating the product (overlap) of arbitrary two functions with respect to a variable which are shifted by a certain amount about the variable. That is, when we define the object functions f, g, an integral variable of the functions X and a relative shift of the two functions x, the cross-correlation function Rfg can be written as the following equation: Rfg=∫f(X)g*(X-x)dX. Note that * denotes complex conjugate. In the case of a microscope image, etc., the functions f and g are real, and then g*(X-x)=g(X-x). If the two object functions are the same, the cross-correlation function is reduced to the auto-correlation function. If the value of Rfg is large, it indicates that the two functions (or patterns) are similar to each other. If Rfg takes a large value for a certain value of x, the relative shift between the two functions is obtained. For example, when the cross-correlation function is calculated for two TEM images taken successively, it gives the knowledge about the image drift during the acquisition of the images. (If the value of the correlation function is large for a small value of x, this indicates a small image drift.) For high-speed computer calculation of the cross-correlation function, FFT (fast Fourier transform) is used on the basis of the following theorem: Fourier transform of the product of certain functions is equivalent to the product of Fourier transforms of the respective functions. That is, the cross-correlation function is calculated by the inverse Fourier transform of the power of the Fourier transforms of the respective functions.
Related term auto-correlation function
10. first principle calculation
"First principle calculation" is a method to calculate physical properties directly from basic physical quantities such as the mass and charge, Coulomb force of an electron, etc. based on the principle of quantum mechanics. In other words, the calculation derives physical properties directly from the basic principle without introducing adjusting parameters or modeling which are used to find agreement between theoretical calculations and experimental results. Starting from the Coulomb interaction between electrons, atomic nuclei and electron-atomic nucleus, the properties of materials (mainly electronic properties) are non-empirically calculated. Along with the great improvement of the computer performance, the calculations for systems containing many atoms have become possible with lower cost and high speed, thus the method is increasingly prevailing. The method is indispensable for predicting properties of new materials and of understanding properties of existing materials. In the TEM field, the method is used for the study of fine structures of EELS spectra that reflect the density of states of materials.
Related term electron energy-loss spectroscopy, EELS
11. deconvolution
11-1. Fourier-log deconvolution
"Fourier-log deconvolution" is a method to obtain a single scattering spectrum of EELS from an experimental spectrum by eliminating the multiple-scattering effect, where multiple-scattering is assumed to obey the Poisson distribution. R.F. Egerton has introduced the method to the spectrum processing of EELS. Fourier-log analysis has also been used in the signal processing of sound waves.
11-2. deconvolution
"Deconvolution" is a method to eliminate spectral blur due to an instrument function. An observed spectrum is given by the convolution of a true spectrum and an instrument function. Fourier transform of the observed spectrum is expressed by the product of the Fourier transform of the true spectrum and the Fourier transform of the instrument function. Thus, the resultant Fourier transform of the true spectrum is obtained by dividing the Fourier transform of the observed spectrum by the Fourier transform of the instrument function. Then, the true spectrum is obtained by the inverse Fourier transform of the obtained Fourier transform of the true spectrum. The deconvolution method is used by combining the Fourier-log method, the maximum entropy method (MEM) or the Richardson-Lucy method.
Related term Fourier-log deconvolution, maximum entropy method, MEM
12. radial distribution function
A diffraction pattern (halo pattern) is taken from an isotropic amorphous substance. From the intensity distribution curve of the pattern, the smooth background passing through the center of the wavy curve is subtracted to remove only the interference term between different atoms. The "radial distribution function" is obtained by the Fourier transform of the interference term. The average interatomic distance (or the distribution of the interatomic distance), the coordination number and the density of the substance can be examined from the function.
13. noise filter
A filter that removes noise components from various frequency components.
14. high-pass filter
A filter that passes only frequency components higher than a certain frequency.
Related term low-pass filter
15. curve fitting
"Curve fitting" is to decompose an entire spectrum into the sum of the component spectra. It is frequently used in spectroscopic analysis.
Related term Gaussian function, Lorentzian function, mixed Gaussian/Lorentzian function, least-squares method
16. Hough transform
"Hough transform" is a method to transform a certain line in an image into one point. In analysis of lattice strain by CBED, the lattice strain is determined in such a way that the positions of experimental HOLZ lines are reproduced by computer simulation of the lines with changing lattice parameters. In this determination, if the HOLZ lines are expressed as points (Cartesian coordinates) by the Hough transform, computer programming for fitting can be facilitated.
17. Fourier synthesis
"Fourier synthesis" is a method that adds the phase to the amplitude of diffraction spots and takes the sum of many reflections in crystal structure analysis. This method enables us to obtain the electron density in a real space in X-ray diffraction, and also in electron diffraction where kinematical diffraction can be applied (for example, for biological specimens such as proteins), we can obtain the electron density from the same method. Furthermore, in the structure analysis using electron diffraction, Fourier synthesis enables us to obtain the crystal potential distribution. Finding the crystal potential allows the electron density to be mathematically obtained. In the case of specimens in material science applications, the structure analysis is performed by CBED since these specimens have strong dynamical effects.
Related term convergent-beam electron diffraction, CBED
18. Fourier transform
18-1. Fourier transform
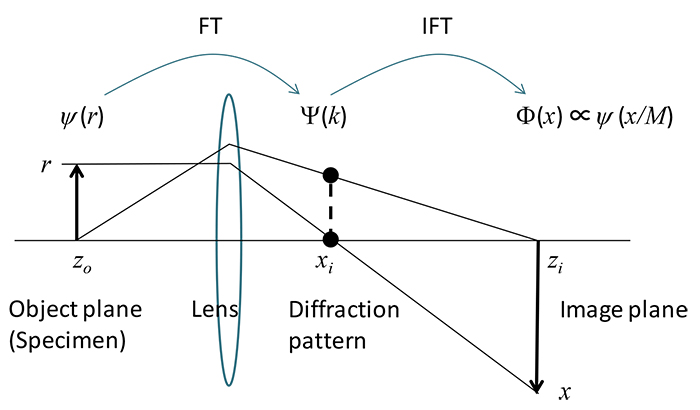
A method that transforms a function of certain variables into a function of the variables conjugate to the certain variables. For example, "Fourier transform" is used for light or sound as a function of time to express it as a function of frequency (spectral analysis), or for scattered waves from an object or a crystal potential as a function of position to transform it into a diffraction pattern or crystal structure factors as a function of wavenumber. The imaging lens system of a TEM can be considered as a system in which scattered waves from an object or a crystal potential are Fourier transformed into a diffraction pattern and subsequently inverse Fourier transformed to an image of the object, where the assumption of Fraunhofer diffraction is applied.
Here, ψ(r) stands for the scattered waves from the specimen, being a function of the real space r, and Ψ(k) for the diffracted waves formed on the back focal plane of the imaging lens, being a function of the reciprocal space k [1/m]. The first equation expresses Fourier transform. That is, the scattered waves ψ(r) produced by the specimen are transformed to a diffraction pattern Ψ(k). The second equation expresses inverse Fourier transform. That is, the diffraction pattern Ψ(k) is transformed to a specimen’s image ψ(r).
Fig. 1 TEM imaging by a lens (image and diffraction pattern) The imaging process of a transmission electron microscope can be considered as a series of Fourier transform from scattered waves from a specimen to a diffraction pattern and of inverse Fourier transform of the diffraction pattern to an image of the specimen. ψ(r) expresses scattered waves of the specimen, being the function of position r, and Ψ(k) expresses diffracted waves formed on the back focal plane of the imaging lens, being a function of the wave number k [1/m]. Φ(x)∝ψ(x/M) expresses the scattered waves on the imaging plane, which is an image of the specimen, being the function of position r. It is noted that Φ(x) is equal to ψ(r) shown in the second equation, except for a magnification M and image inversion caused by the lens.
Fig. 2 (a) Diffraction pattern (Fourier transform pattern) of an Au crystal. (b) Crystal lattice image of the Au crystal and its FFT pattern. Accelerating voltage: 300 kV. Periodicities of the crystal lattice appear as bright diffraction spots on the back focal plane of the lens depending on the spacing and orientation of the lattice, by Fourier transform (a). A magnified image of the crystal lattice is obtained from the diffraction spots by inverse Fourier transform (imaging process of the lens) (b).
Related term inverse Fourier transform, Fourier synthesis
18-2.fast Fourier transform
A computing method to decrease the calculation time of a Fourier transform. Since "fast Fourier transform (FFT)" is executed using a computer, calculations are performed by a discrete finite sum, instead by an integration. It greatly decreases the computation time by dividing the calculation into certain sub-groups and by changing the order of the calculation. In a discrete Fourier transform with a period of N, the number of operation is normally proportional to N2 but it is decreased to N log N in FFT. This method is used for analysis of high-resolution images.
Related term Young fringe
18-3.inverse Fourier transform
Fourier transform is a method that transforms a function of certain variables into the function of the variables conjugate to the certain variables. On the other hand, "inverse Fourier transform" is a method that transforms the Fourier-transformed function into a function of the original variable. For example, when a crystal potential as a function of position is Fourier-transformed, crystal structure factors are obtained as a function of wavenumber. Next, when the crystal structure factors are inverse-Fourier-transformed, the crystal potential as the function of position is obtained. In TEM imaging, Fourier transform and inverse Fourier transform of the specimen are automatically executed, so that the diffraction pattern and structure image are obtained at the back focal plane and the image plane, respectively.
Related term Fourier transform
19. Fourier mask
The "Fourier mask" is a mask inserted on the diffraction plane to remove the noise of a lattice image or a structure image, allowing only diffraction spots to pass and background noise between the diffraction spots to be cut.
20. smoothing
"Smoothing" is to perform an averaging of data and to obtain a smoothly connected data set (smooth curve) by eliminating singular points and noises from a series of data with the help of the data at the neighboring points. For a simple example, a data at a certain point is replaced by the average between the data at the point and the data of the nearest neighbor points. Smoothing is frequently used for image processing and processing of spectroscopic data.
21. maximum entropy method
"Maximum entropy method (MEM)" is a method, which originates from the information theory, to deduce the most provable solution through maximizing the information entropy when information (measurement) is insufficient. It is well known that it has been successfully applied to the crystal structure analysis by X-ray powder diffraction. For TEM, it is used in the case of EELS spectra, to obtain the inherent spectra by removing the effect of the energy spread of the incident electron beam.
22. Monte Carlo method
"Monte Carlo method" is a comprehensive term of random statistical sampling techniques that are used to solve a deterministic or probabilistic problem. This method is used for the simulation of the process where the incident electrons are scattered and spread within a specimen. As the energy of the incident electron beam is larger, the spread of the incident electrons is larger. As the atomic number and density are larger, the spread of the incident electrons is smaller, For example, Monte Carlo method is effectively used to obtain the atomic number effect in quantitative analysis in characteristic X-ray spectroscopy.
Related term atomic-number effect
23. Radon transform
Fourier transform executes transformation of the function of Cartesian coordinates (x, y) into the function of the variables conjugate to the original Cartesian coordinates. On the other hand, "Radon transform" executes transformation of the function of a two-dimensional polar coordinates (r, θ) into the function of the variables conjugate to the original two-dimensional polar coordinates. This transformation is used for tomography, which reconstructs the three-dimensional structure of a specimen from electron microscope images taken at many different orientations of the incident electron.
Related term tomography
24. Richardson-Lucy method
The Richardson-Lucy method is used in combination with the deconvolution method which is one of image processing methods. The deconvolution method is based on the concept where an observed image is expressed by convolution of a true image and a Point Spread Function (PSF) that causes degradation of the image. The true image is obtained from deconvolution of the observed image and the PSF. However, if the PSF is not known, the estimation of the PSF is required. The Richardson-Lucy method is effective for estimating the PSF. (Another method that can be used in combination with convolution is the maximum entropy method.) In deconvolution using the Richardson-Lucy method, first the initial true image is assumed. The PSF is obtained from the deconvolution of the observed image using the true image. Then, the second-generation true image is obtained from the deconvolution of the obtained image using the obtained PSF. The final true image is obtained by repeating these processes. That is, these processes are executed iteratively until the image is converged. For example, the method is used for enhancing an EELS spectrum.
Related term deconvolution
25. low-pass filter
A filter that passes only frequency components lower than a certain frequency.
Related term high-pass filter
26. Lorentzian function
26-1. Lorentzian function
"Lorentzian function" is a function given by (1/π){b / [(x - a)2 + b2]}, where a and b are constants. It is used for pre-processing of the background in a spectrum and for fitting of the spectral intensity. The real spectral shapes are better approximated by the Lorentzian function than the Gaussian function.
Related term curve fitting, Gaussian function
26-2. mixed Gaussian/Lorentzian function
"Mixed Gaussian-Lorentzian function" is a function composed of a Gaussian and a Lorentzian function. It is used for pre-processing of the background in a spectrum and for fitting of the spectral intensity when the both functions are inappropriate to reproduce an experimental spectrum.
Related term curve fitting, Gaussian function, Lorentzian function
27. Fourier Shell Correlation, FSC
Fourier Shell Correlation (FSC) is a measure of reliability of the three-dimensional (3D) structures of biological macromolecules obtained by “single particle analysis”. FSC is expressed as a function of spatial frequency by the following equation (normalized cross correlation).
Here, F1(k) and F2(k)are 3D Fourier transforms of the two structures reconstructed from arbitrary two independent sets of TEM images obtained. F2(k)* is a complex conjugate of F2(k), and Σk,ΔkF(k) means summing up F(k) over a small range Δk around k. FSC (k) takes a value between +1 and –1 for every spatial frequency k. The value of FSC (k) close to +1 means that the two reconstructed structures agree well, indicating a high degree of reliability of the obtained structure. If FSC does not decrease monotonically with spatial frequency k at high frequencies, the reliability of the FSC function is considered to be low. The following example shows the FSC and spatial resolution for mouse apoferritin. First, a data set of TEM images acquired for single particle analysis is randomly divided into two groups, and two independent 3D structures are obtained by image-processing analysis for each group. FSC is calculated using the two obtained 3D structures. Fig. 1(a) shows a 3D density map of apoferritin reconstructed from 120,295 particles extracted from 840 cryo-TEM images. Fig. 1(b) is the FSC calculated for this 3D density map. The values of FSC at low frequencies are close to +1 and damped with increasing frequency monotonically towards 0. This behavior confirms high reliability of the FSC function. In single particle analysis, it is common to define the spatial resolution of the obtained structure to be the reciprocal of the spatial frequency at which FSC = 0.143. (The value “0.143” is a value adopted based on statistical discussion about the correlation of random noise and on referring the resolution defined for X-ray crystallography.) The resolution for apoferritin was determined to be 0.153 nm from a spatial frequency of 6.5 nm-1 at which FSC takes a value of 0.143.
(Proofread by Specially Appointed Professor Keichi Namba, Osaka University)
Fig1. 3D density map of mouse apoferritin obtained by single particle analysis and its FSC. (a) 3D density map. (b) An FSC function calculated from the two 3D density maps. The resolution was determined to be 0.153 nm from a spatial frequency of 6.5 nm-1 at which FSC = 0.143.